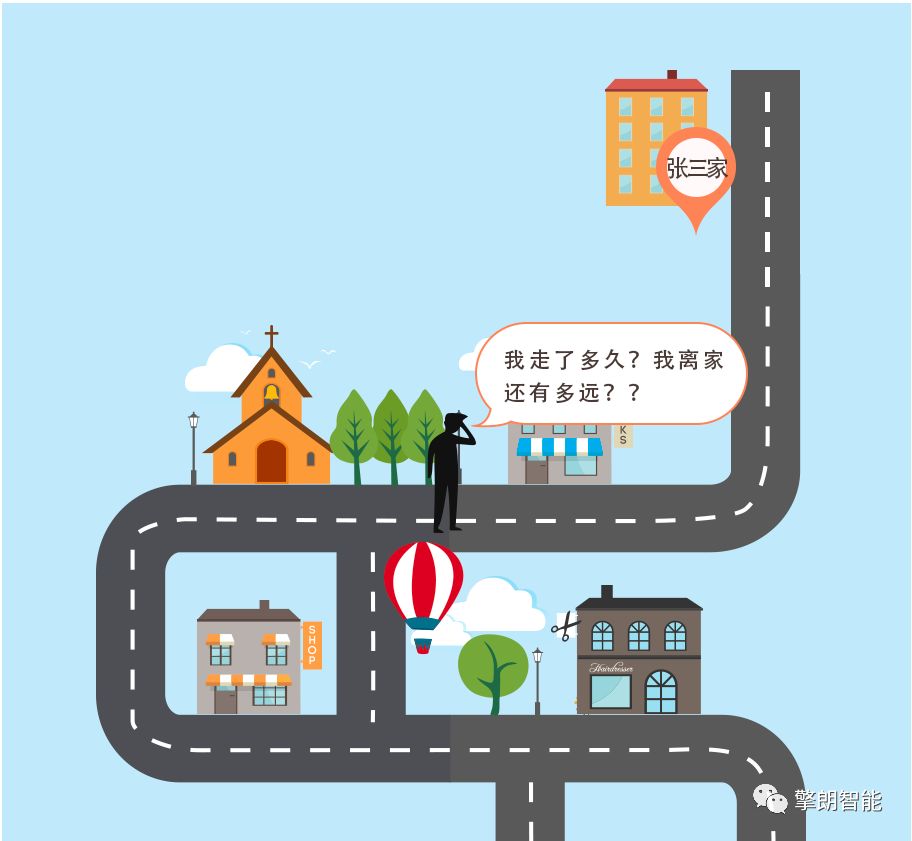
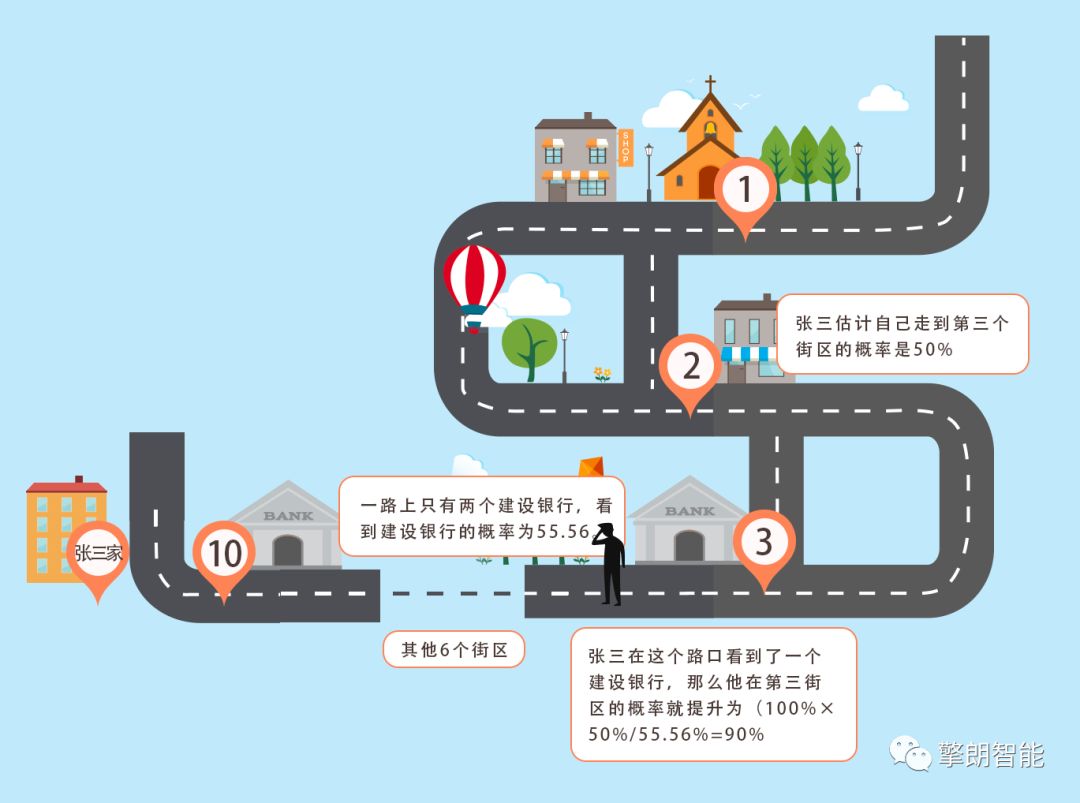
"As intelligent service robots have gradually become the cusp of the industry, mobile robots are increasingly appearing around people. I believe that with the continuous improvement of sensing technology, intelligent technology and computing technology, intelligent mobile robots will definitely be able to produce The SLAM technology, which plays a key role in autonomous positioning and navigation technology, has also become the focus of attention. So, what is SLAM technology? How is SLAM technology realized? Its core steps What are the difficulties? Today, the editor will come to talk with you about the SLAM technology that plays an important role in the autonomous movement of robots." What is SLAM technology? SLAM is the abbreviation of Simultaneous Localization And Mapping, which was first proposed by Hugh Durrant-Whyte and John J. Leonard in 1988. SLAM is not so much an algorithm as it is a more appropriate concept. It is defined as a solution to "the robot starts from an unknown location in an unknown environment and repetitively observes map features (such as wall corners, pillars, etc.) during movement. Locate one's own position and posture, and then build a map incrementally according to one's own position, so as to achieve the purpose of simultaneous positioning and map construction." The core steps of SLAM technology Generally speaking, SLAM includes three processes: perception, positioning, and mapping. Perception-The robot can obtain information about the surrounding environment through sensors. Positioning-through the current and historical information obtained by the sensor, infer its own position and posture. Mapping-based on one's own posture and the information obtained by the sensor, depict the appearance of one's own environment. For example, one day Zhang San was drinking with his friends. Zhang San drank too much, and Li Si sent him home, but he didn't have Zhang San's key. What should I do? I had to send him back to his home. So the question is, after Zhang San wakes up the next morning, how can he know whose house he is in? This question is very simple, just look at the environment around the house. Yes, the process of Zhang San observing the house information is the process of perception. At this time, Zhang San needs to extract information that is valid for him in the house, such as the area of ​​the house, the color of the walls, the characteristics of the furniture, etc. If you are lucky, look. By the time Li Si himself, he basically knew whose house he was in. This process of determining who is in the house is positioning. Then, when Zhang San realized that he was in the Li Sijia, he naturally associated the "Li Sijia" with the characteristics observed by Li Sijia. This is the picture construction. After waking up, Zhang San came out of Li Si’s house. On the way home, Zhang San observed the surrounding environment and estimated how many blocks he walked (positioning), and generated the surrounding environment in his mind all the way. (Building a map). The above are the core steps of SLAM. From the above example, it can be found that perception is a necessary condition for SLAM, and only when the information of the surrounding environment is sensed can it be reliably positioned and constructed a map of the environment. However, positioning and mapping are an interdependent process: positioning relies on known map information. Only when Zhang San knows the location of Li Sijia can he know the distance from Li Sijia; mapping depends on reliable positioning. After knowing how far away I was, I knew the distance between the China Construction Bank on the left and Li Sijia. Of course, the data for positioning and mapping must include the relative displacement of Zhang San's observation and perception along the way and the correction to the displacement. Having said so much nonsense, I feel that SLAM is actually not very complicated. Yes, this is because the human brain is very smart and subconsciously solves the core problem in SLAM-feature extraction and tracking, and optimal posterior estimation. . The core problem of SLAM Generally speaking, the SLAM problem can be basically divided into two parts: the front-end and the back-end. The front end mainly processes the data obtained by the sensor and transforms it into relative pose or other forms that the robot can understand; the back end mainly deals with the problem of optimal posterior estimation, that is, the optimal estimation of pose, map, etc. The sensors possessed by the robot mainly include: depth sensors (ultrasonic, lidar, stereo vision, etc.), vision sensors (cameras, beacons), inertial sensors (gyros, encoders, electronic compasses) and absolute coordinates (WUB, GPS) Wait. Unlike human perception of the environment, the information that the robot obtains from these sensors is very limited and cannot fully characterize the environment around the robot. For example, the commonly used 2D lidar can only obtain the depth information of a plane; the image data obtained by the camera can not fully distinguish the attributes, characteristics and even other associations of each object like the human brain. As shown in the figure above, the situation seen in the human field of vision is shown in figure (1), but for a robot equipped with only 2D lidar, the world it sees is the same as in figure (2) . Therefore, how the front-end can obtain more effective information fully and reliably has always been a topic studied by many SLAM researchers. At the same time, the sensor will have noise, whether it is the inherent noise of the sensor itself or the wrong data obtained, it will affect the SLAM. Therefore, another core problem of SLAM is: how to best estimate the pose and map information of the robot from these noisy information. The current methods of SLAM processing the back-end can be roughly divided into two categories: methods based on probability models and methods based on optimization. SLAM based on probabilistic model is the more mainstream method in 2D-SLAM, and the more representative ones are EKF, UKF, and PF. The research in this area has been relatively mature and has been gradually applied in business scenarios; Based on optimization is the mainstream direction of SLAM research in recent years, most of it is applied in the field of VSLAM, with TORO, G2O, etc. being representative. The realization method of SLAM technology As mentioned above, the mainstream methods of SLAM back-end optimization are currently mainly divided into methods based on probability models and methods based on optimization. As the classic method of SLAM in the "classical period", SLAM based on probabilistic model has a very complete theoretical system, and with its excellent performance, it is still active in the SLAM application field. As a must-learn classic for introductory SLAM, the editor will give you a general introduction to the SLAM method based on the probability model. SLAM based on probabilistic models can basically be derived from Bayesian estimation. In layman's terms, Bayesian estimation is based on the prior probability of hypothesis, the probability of different data observed under a given hypothesis, and the observed data itself. The method of finding the posterior probability. The formula is as follows: It may be a little embarrassing to see this, let us once again invite student Zhang San to demonstrate on-site for everyone. It didn't take long for Zhang San to walk out of Li Si's house. Because he hadn't woken up much, he didn't remember how many blocks he had walked. At this time, Zhang San found out that there was a construction bank on his right, so he could guess how many blocks he walked. Next, Zhang San offered the legendary "Bayesian Estimation" Dafa to calculate the probability that he would be in each block after seeing a Construction Bank on his right, marked as p(A|B) . The effective information used by Zhang San to estimate his position is the event that there is a Construction Bank on the right hand side. Assuming that the probability that Zhang San sees a Construction Bank on the right hand side is recorded as p(B), then the conditional probability p(B|Ai) is The meaning is to assume that Zhang San is in the i-th block and sees the probability of the Construction Bank on his right. The meaning of p(Ai) is the probability that Zhang San is in the i-th block. There are ten blocks from Zhang San to Li Sijia, and the probability of being in the third block is p(A3)=10%. But if you observe that there is a China Construction Bank on the right hand side, it is different: there are two construction banks along the way, so the probability of seeing China Construction Bank this way is p(B)=2/10=20%, but suppose you are in the third Block, then the probability of seeing CCB is p(B|A3)=100%. Then, with the observation of China Construction Bank, the probability that Zhang San is in the third block increases to 100%×10%/20%=50%. If Zhang San is more confident that he has not observed that the probability of being in the third block before CCB is 50%, and the probability of the remaining blocks is evenly distributed, then the probability of seeing CCB all the way p(B)=100%×50%+100%×5.55%+0%×5.55%×8=55.55%, After observing the results of China Construction Bank, the probability that Zhang San is in the fourth block has risen to: 100%×50%/55.55%=90%. It can be seen that Bayesian estimation provides a method of obtaining posterior estimation by combining a priori estimation with observation information. Having said that, how exactly is Bayesian estimation applied to the SLAM method? For a classic SLAM problem, suppose xt is the state quantity at time t, z1:t is the observed quantity at time, u1:t is the control quantity at time 1:t, and m is the map. Then the SLAM needs to be solved in the known In the case of control quantity and observation probability distribution, the robot's pose state and the map optimal estimation problem. which is: Since p(zt|z1:t-1,u1:t) does not depend on x, it is the same for any posterior probability p(zt|z1:t-1,u1:t) and can be regarded as a constant. It is assumed here that the state transition of the system model obeys the first-order Markov model, that is, the current state xt is only related to the previous state xt-1, so: According to equations (2) and (3), under the assumption of the first-order Markov model, Bayesian estimation can transform the current state and the optimal posterior estimate of the map into the assumed conditional probability and state of the observation data The transfer equation and the function of the posterior estimate of the previous state. Therefore, the optimal posterior estimation of the state and map can be solved iteratively. The above is an example of a classic SLAM problem. There are many ways to answer this type of problem, such as the classic Kalman filter (KF), extended Kalman filter (EKF), unscented Kalman filter (UKF), and RB particle filter. (FastSLAM) and information filtering (SEIF) and so on. They are all methods of solving SLAM problems based on probability models, and their essence is to find the optimal posterior estimation. The above is the preliminary content of the SLAM algorithm in this issue. In fact, there is still a lot of work to be done to realize the robot's motion function in practice through the SLAM algorithm. Right Angle DIP Centronic Connector
Right Angle DIP Centronic Connector.
Current Rating:5A Right Angle DIP Centronic Connector ShenZhen Antenk Electronics Co,Ltd , https://www.atkconnectors.com

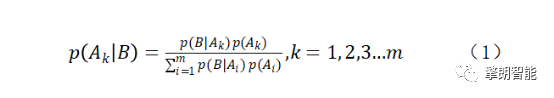
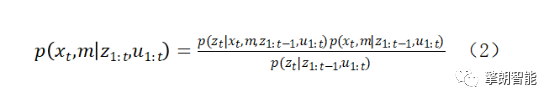
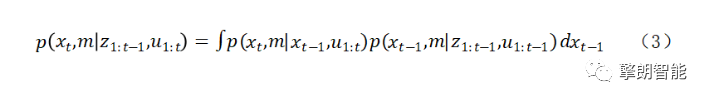
Dielectric Withstanding Voltage:1000V for one minute
Insulation Resistance:1000MΩ Min.(at 500V DC)
Contact Resistance:35mΩ Max.
Temperature:-55°C to +105°C